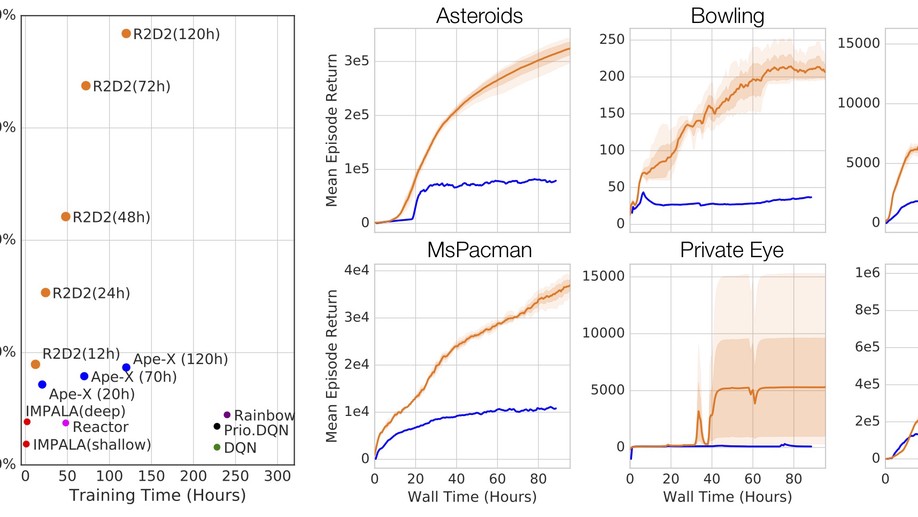
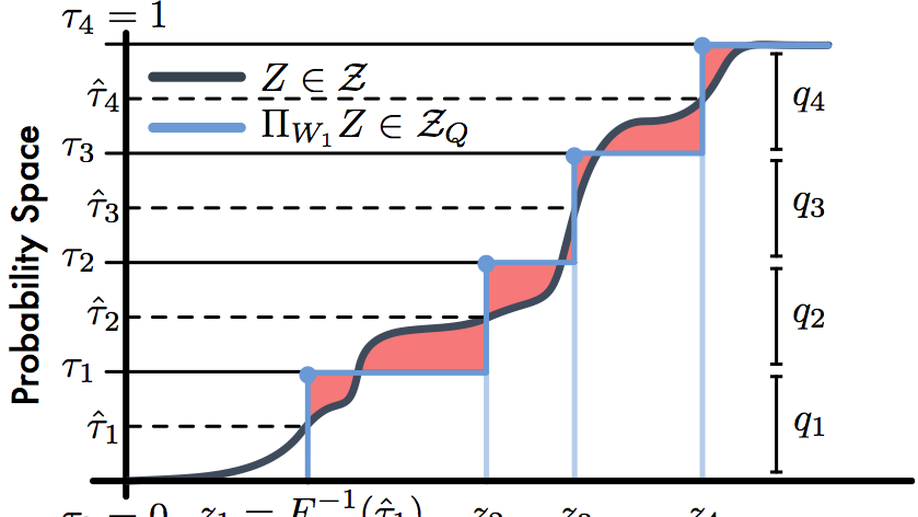
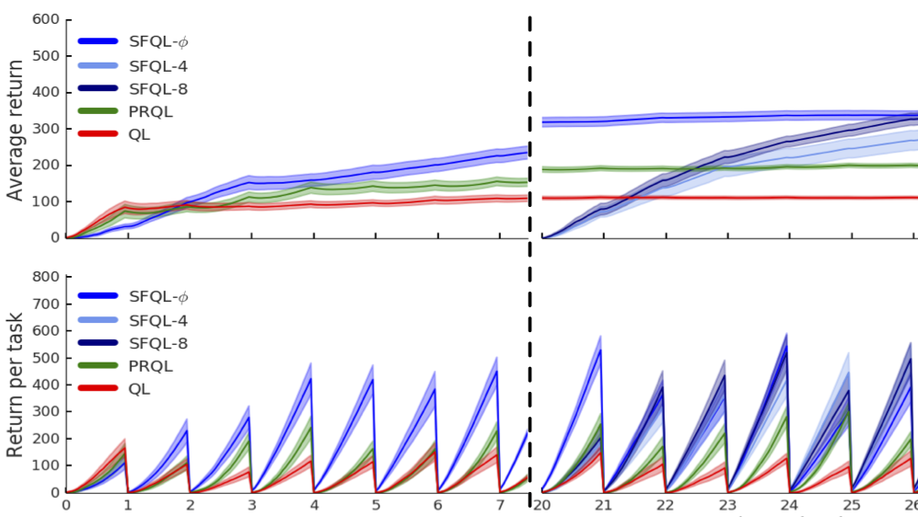
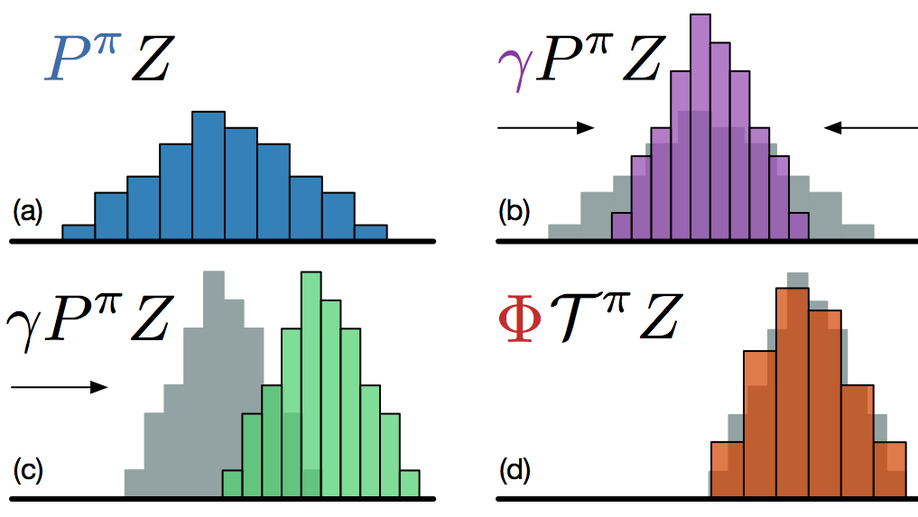
Will Dabney
Research Scientist
DeepMind
Biography
Currently, I am a senior staff research scientist at DeepMind, where I study reinforcement learning with forays into other topics in machine learning and neuroscience.
My research agenda focuses on finding the critical path to human-level AI. I believe we are in fact only a handful of great papers away from the most significant breakthrough in human history. With the help of my collaborators, I hope to move us closer; one paper, experiment, or conversation at a time.
Interests
- Distributional RL
- Foundations of deep RL
- Connecting Neuroscience & AI
- Learning from sparse rewards
Education
PhD in Computer Science, 2014
University of Massachusetts, Amherst
BSc in Computer Science, 2007
University of Oklahoma
BSc in Mathematics, 2007
University of Oklahoma